Gymnasiasten bei der Prüfung Mathe-Abi in Sachsen-Anhalt: Sind Sie klüger als ein Zwölftklässler?
Am Freitag, 9. Mai, steht das Mathe-Abitur in Sachsen-Anhalt an – für viele der härteste Prüfungstag überhaupt. Wir zeigen ausgewählte Originalaufgaben aus dem vergangenen Jahrgang. Wer kann die Aufgaben knacken? Rechnen Sie mit.
Magdeburg/Halle (Saale). Rund 5.400 Schülerinnen und Schüler schreiben aktuell ihr Abitur in Sachsen-Anhalt. Seit Anfang April laufen die schriftlichen Prüfungen – am 9. Mai folgt mit Mathematik das Fach, das oft als die größte Hürde gilt.
Lesen Sie auch: Angst vor Mathe: So bereitet Expertin an Hochschule Harz Abiturienten auf Prüfung vor
So läuft das Mathe-Abitur ab
Das Mathematik-Abitur besteht aus zwei Prüfungsteilen: einem Wahlteil und einem Pflichtteil, jeweils mit Aufgaben aus Analysis, Analytischer Geometrie und Stochastik.
Lesen Sie auch: Das hat sich beim Deutsch-Abitur in Sachsen-Anhalt 2025 geändert
Je nach Anforderungsniveau (grundlegend oder erhöht) haben die Prüflinge 255 bzw. 300 Minuten Zeit – Zeichengeräte, Taschenrechner und Formelsammlungen sind nur teilweise erlaubt.
Lesen Sie auch: Abiturprüfungen beginnen in Sachsen-Anhalt
Erläuterung: „BE“ steht in diesem Zusammenhang mit Prüfungsaufgaben für „Bewertungseinheit(en)“.
Mathe-Abi-Aufgaben 2024: Sind Sie bereit?
Wir haben echte Aufgaben aus dem Abiturjahrgang 2024 recherchiert! Stellen Sie sich den Prüfungsfragen und finden Sie heraus, ob Sie den Mathetest bestehen würden.
Auch interessant: Abiturprüfungen: Landesschülerrat beklagt unfaire Abiturtermine
MATHEMATIK (GRUNDLEGENDES ANFORDERUNGSNIVEAU)
Prüfungsaufgabe Prüfungsteil 1
Pflichtaufgabe
1. Gegeben ist die in R definierte Funktion f mit (x) = x3 – 4x.
a) Begründen Sie, dass der Graph von f symmetrisch bezüglich des Koordinatenursprungs ist. 1BE
b) Der Graph von f und die x-Achse schließen eine Fläche ein, die aus zwei Flächenstücken besteht. Berechnen Sie den Inhalt dieser Fläche. 4BE
Das könnte Sie auch interessieren: Das sind die 20 besten Schulen Deutschlands - Auch Halle im Rennen
Wahlpflichtaufgabe
4.3 Auf einer Spendengala wird das folgende Spiel angeboten: Für einen Einsatz von 3 Euro dreht der Spieler zweimal ein Glücksrad. Dieses besteht aus mehreren gleich großen Sektoren. 10 % der Sektoren sind grün eingefärbt. Für jedes Erzielen eines grünen Sektors werden dem Spieler 10 Euro ausgezahlt.
a) Zeigen Sie, dass die Wahrscheinlichkeit dafür, bei diesem Spiel genau einmal einen grünen Sektor zu erzielen, 18 % beträgt. 2BE
b) Begründen Sie, dass der Veranstalter der Spendengala erwarten kann, mit diesem Spiel auf lange Sicht mehr Geld einzunehmen als auszuzahlen. 3BE
MATHEMATIK (GRUNDLEGENDES ANFORDERUNGSNIVEAU)
Prüfungsaufgabe Prüfungsteil 2
Aufgabe 1: Analysis
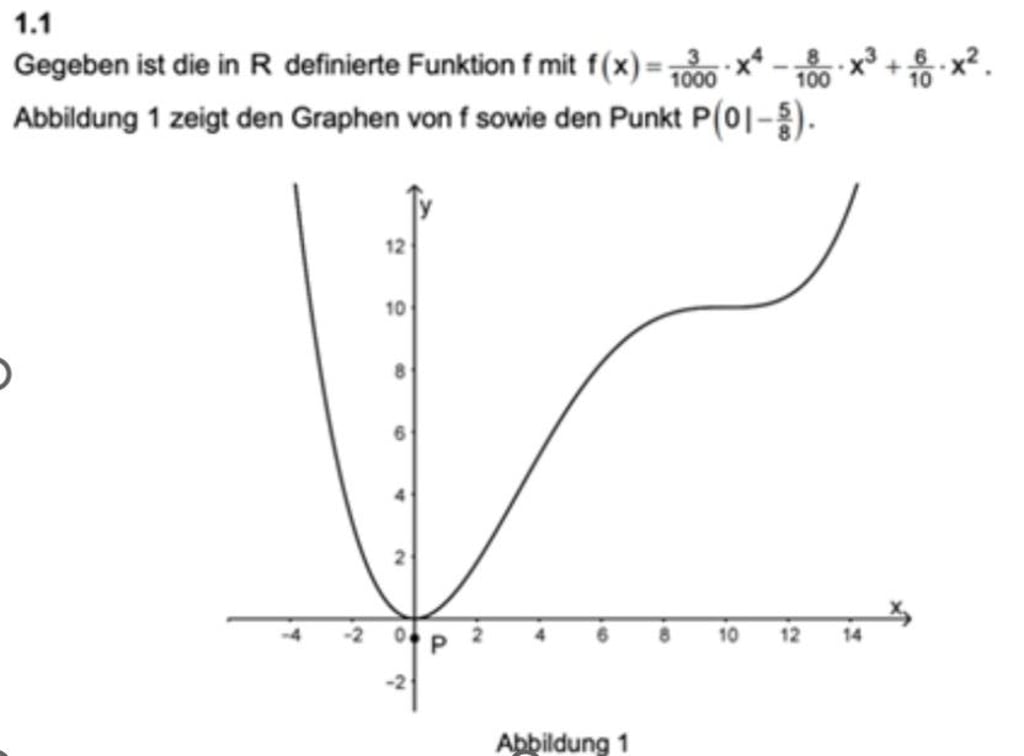
a) Geben Sie die Koordinaten des Tiefpunkts des Graphen von f an. Zeigen Sie rechnerisch, dass der Graph von f keine weiteren Extrempunkte besitzt. 6 Die Tangente an den Graphen von f im Punkt (5|f (5)) wird mit t bezeichnet. 6BE
Lesen Sie auch: Sachsen-Anhalts Bildungsministerium untersagt Gender-Sternchen in Schulen
b) Ermitteln Sie eine Gleichung von t. 4BE
c) Skizzieren Sie in Abbildung 1 zwei von t verschiedene Tangenten an den Graphen von f, die die y-Achse im Punkt P schneiden und deren Steigungen unterschiedliche Vorzeichen haben. 3BE
Aufgabe 2: Analytische Geometrie
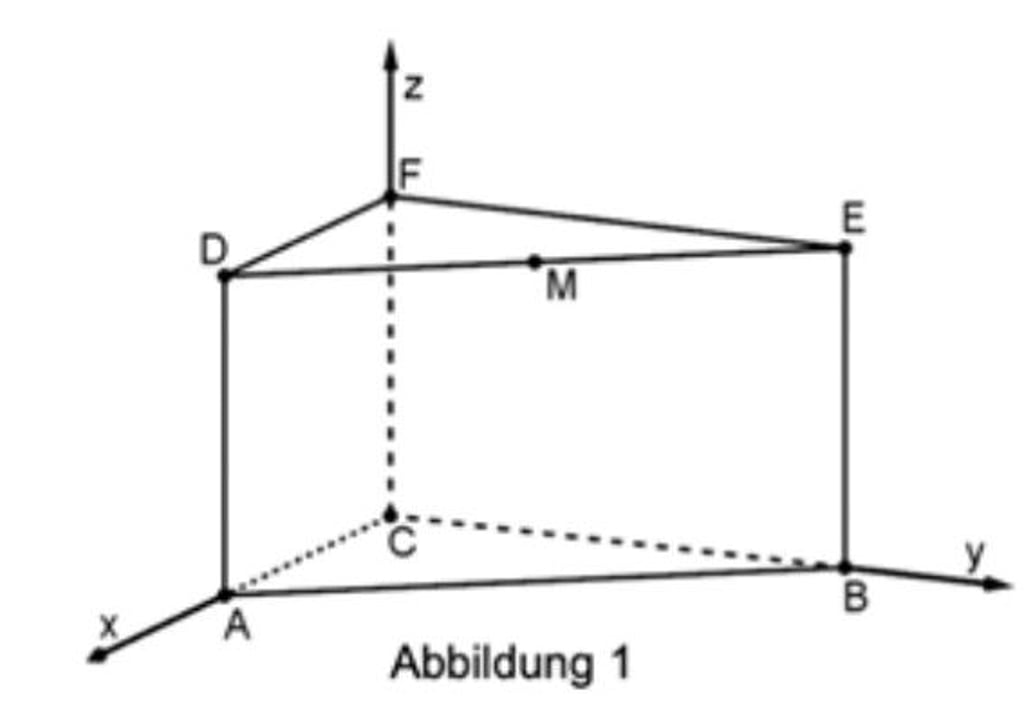
Gegeben sind das gerade Prisma ABCDEF mit den Eckpunkten C (0|0|0) , D (6|0|5), E (0|8|5) und F (0|0|5) sowie der Punkt M (3|4|5) (siehe Abbildung 1).
a) Berechnen Sie den Oberflächeninhalt des Prismas. 4BE
b) Begründen Sie, dass die Punkte D, E und F auf einem Kreis mit dem Mittelpunkt M liegen. 3BE
Aufgabe 3: Stochastik
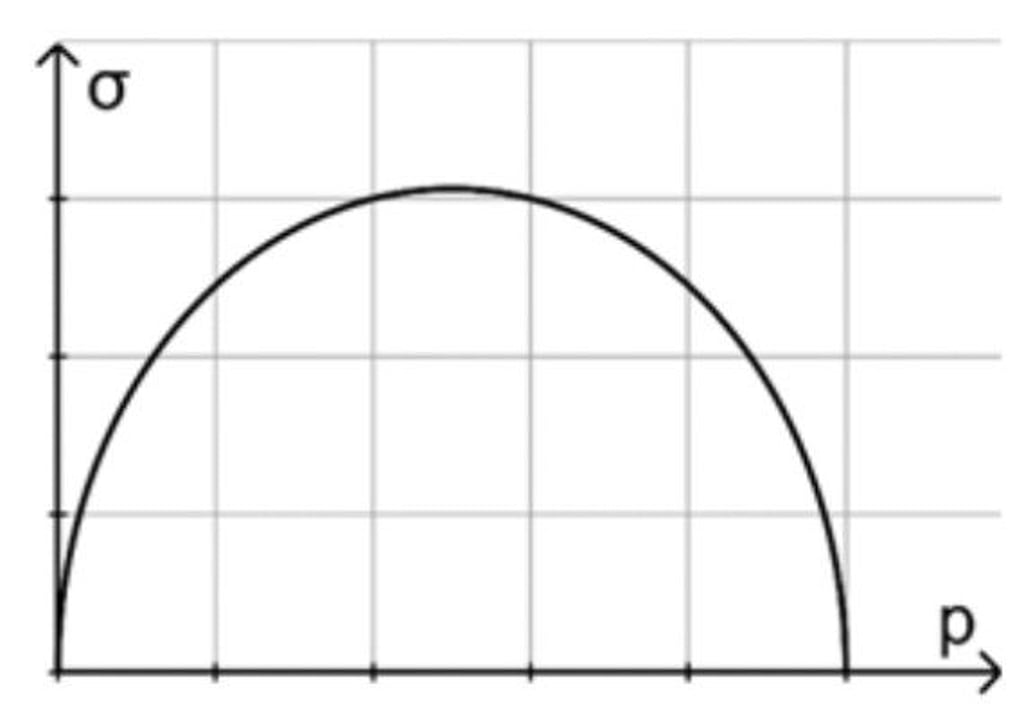
3.3 Für binomialverteilte Zufallsgrößen mit den Parametern n = 15000 und p ist in der Abbildung die Standardabweichung σ in Abhängigkeit von p dargestellt. Ergänzen Sie im dargestellten Koordinatensystem die Skalierungen der Achsen und erläutern Sie Ihr Vorgehen.
MATHEMATIK (ERHÖHTES ANFORDERUNGSNIVEAU)
Prüfungsaufgabe Prüfungsteil 1
Pflichtaufgabe
1. Gegeben ist die Funktion f mit (x) = 12⋅ 1x12⋅ 1x , x ∈ R, x ≠ 0.
a) Berechnen Sie den Funktionswert der ersten Ableitungsfunktion von f an der Stelle 2. 2BE
b) Ermitteln Sie einen Term derjenigen Stammfunktion von f, deren Graph den Punkt (e2|4) enthält. 3BE
Wahlpflichtaufgabe
5.2 Die in R definierte Funktion f hat die erste Ableitungsfunktion f′ mit f‘(x) = 2 ⋅ e ′ und es gilt f (0) = 1. Leitet man die erste Ableitungsfunktion f′ ab, so erhält man die zweite Ableitungsfunktion f′′ von f.
Entsprechend entsteht die hundertste Ableitungsfunktion f(100) von f. Der Graph der hundertsten Ableitungsfunktion f(100) lässt sich aus dem Graphen von f durch eine Verschiebung in x-Richtung erzeugen.
Ermitteln Sie, um wie viele Einheiten der Graph von f dazu in x-Richtung zu verschieben ist. 5BE
MATHEMATIK (ERHÖHTES ANFORDERUNGSNIVEAU)
Prüfungsaufgabe Prüfungsteil 2
Aufgabe 1: Analysis
1.2 Die Leitung eines großen Unternehmens versendet jeden Arbeitstag um 7 Uhr eine E-Mail mit tagesaktuellen Informationen an alle Mitarbeiterinnen und Mitarbeiter. Diese wurden gebeten, nach dem Lesen der E-Mail eine Lesebestätigung zu versenden. Die folgende Tabelle zeigt für einen bestimmten Tag, wie viele Lesebestätigungen bei der Leitung des Unternehmens bis zum jeweiligen Zeitpunkt bereits eingegangen sind.
Beispielsweise sind von 7:00 Uhr bis 10:00 Uhr 4364 Lesebestätigungen eingegangen.
a) Ermitteln Sie mithilfe der Tabelle für den betrachteten Tag, wie viele Lesebestätigungen im Zeitraum von 8.30 Uhr bis 10 Uhr im Mittel pro Stunde eingegangen sind. 3BE
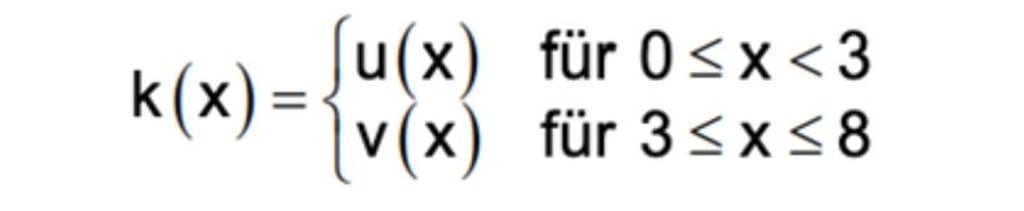
Auf der Grundlage, der über viele Tage erfassten Lesebestätigungen wurde mithilfe der in R definierten Funktionen u und v mit u(x) = 100x3 - 900x2 + 2300x und v (x) = 20x2 -520x + 2880 die Funktion k entwickelt:
Die Funktion k beschreibt modellhaft für einen Zeitraum von acht Stunden eines Arbeitstages die zeitliche Entwicklung der momentanen Änderungsrate der Anzahl der eingegangenen Lesebestätigungen. Dabei ist x die seit 7 Uhr vergangene Zeit in Stunden und k(x) die momentane Änderungsrate der Anzahl der seit 7 Uhr eingegangenen Lesebestätigungen in der Einheit 1/h .
b) Berechnen Sie k(2) und interpretieren Sie das Ergebnis im Sachzusammenhang. 3BE
c) Es gilt v(x) = 20 (x – 18) ⋅ (x - 8). Begründen Sie, dass die Funktion v nicht geeignet ist, die momentane Änderungsrate auch für den Zeitraum nach 15Uhr zu beschreiben. 3BE
d) Berechnen Sie mithilfe der Funktion k die Anzahl der im Zeitraum von 10 Uhr bis 15 Uhr eines Arbeitstages eingegangenen Lesebestätigungen. Ermitteln Sie, um wie viel Prozent diese auf der Grundlage des Modells berechnete Anzahl von der entsprechenden Anzahl des eingangs betrachteten Tages (vergleiche Tabelle) abweicht. 5BE
Aufgabe 2: Analytische Geometrie
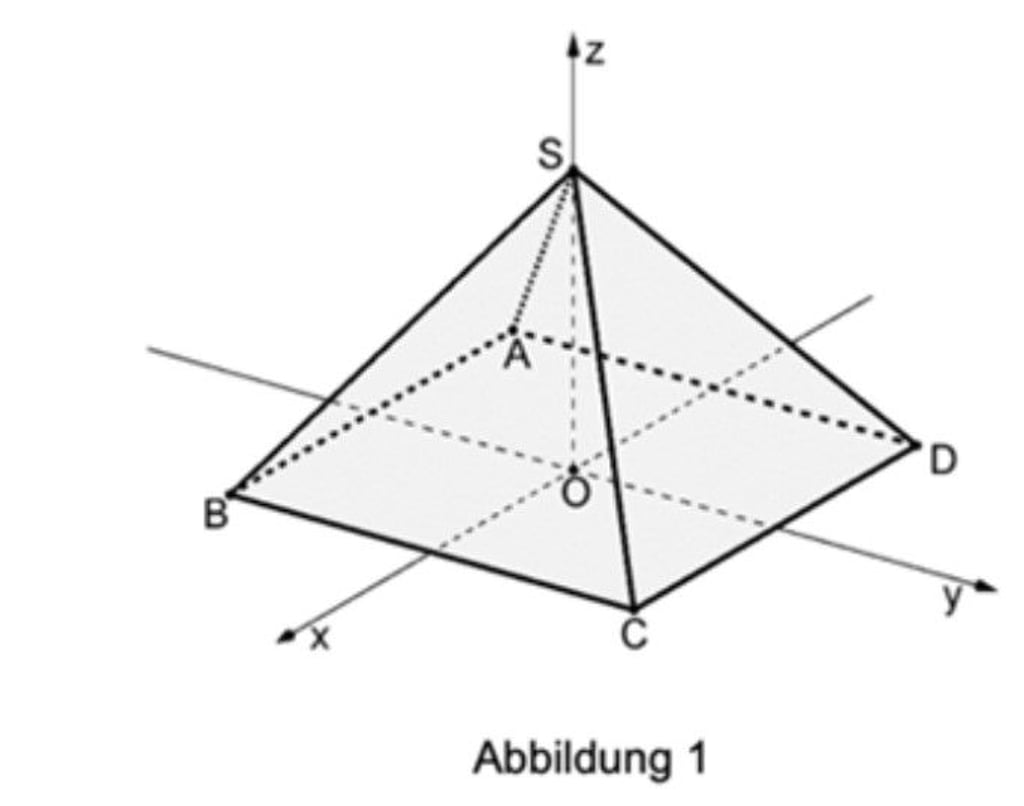
Abbildung 1 zeigt die Pyramide ABCDS mit den Eckpunkten A (-3|-3|0), B (3|-3|0), C (3|3|0), D (-3|3|0) und S (0|0|4) sowie den Punkt O (0|0|0), der in der quadratischen Grundfläche der Pyramide liegt. Die Seitenfläche CDS der Pyramide liegt in der Ebene E.
a) Berechnen Sie den Oberflächeninhalt der Pyramide. 4BE
Abbildung 1 zeigt die Pyramide ABCDS mit den Eckpunkten A (-3|-3|0), B (3|-3|0), C (3|3|0), D (-3|3|0) und S (0|0|4) sowie den Punkt O (0|0|0), der in der quadratischen Grundfläche der Pyramide liegt. Die Seitenfläche CDS der Pyramide liegt in der Ebene E.
a) Berechnen Sie den Oberflächeninhalt der Pyramide. 4BE
b) Genau eine der folgenden Gleichungen (1) bis (3) beschreibt eine Symmetrieebene der Pyramide. Geben Sie diese Gleichung an und begründen Sie für eine der anderen Gleichungen, dass die durch sie beschriebene Ebene keine Symmetrieebene der Pyramide ist. 3BE
(1) x – z = 0 (2) x + y + z = 4 (3) x + y = 0
c) Bestimmen Sie eine Gleichung von E in Koordinatenform. 3BE
[zur Kontrolle: 4y + 3z = 12]
Aufgabe 3: Stochastik
3.1Bei einer statistischen Erhebung werden in einer deutschen Großstadt die privaten Haushalte mit mindestens einem Kind im Vorschulalter betrachtet. Diese werden im Folgenden als „junge Haushalte“ bezeichnet. Es wird festgestellt, dass 60 % der jungen Haushalte mit mindestens einem Pkw ausgestattet sind und 8 % der jungen Haushalte mit mindestens einem Lastenrad. In 14 % der jungen Haushalte ohne Pkw ist mindestens ein Lastenrad vorhanden.
a) Stellen Sie den beschriebenen Sachverhalt in einer vollständig ausgefüllten Vierfeldertafel dar. 4BE
b) Beurteilen Sie für diese Großstadt die folgende Aussage: Die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter junger Haushalt mit mindestens einem Lastenrad ausgestattet ist, ist bei einem jungen Haushalt ohne Pkw mehr als dreimal so groß wie bei einem jungen Haushalt mit mindestens einem Pkw. 3BE